ECC椭圆曲线加密

椭圆曲线加密是非对称加密的一种，与RSA一样，是基于单陷门的加密方式，利用的是离散对数问题。

首先需要知道什么是椭圆曲线，椭圆曲线的表示方法是什么，再就是加密和解密方式。

ECC椭圆曲线表示方法

表达式

y2 = x3 + a x + b

其中要求 ：4 a3 - 27 b2 != 0

大致图像如下：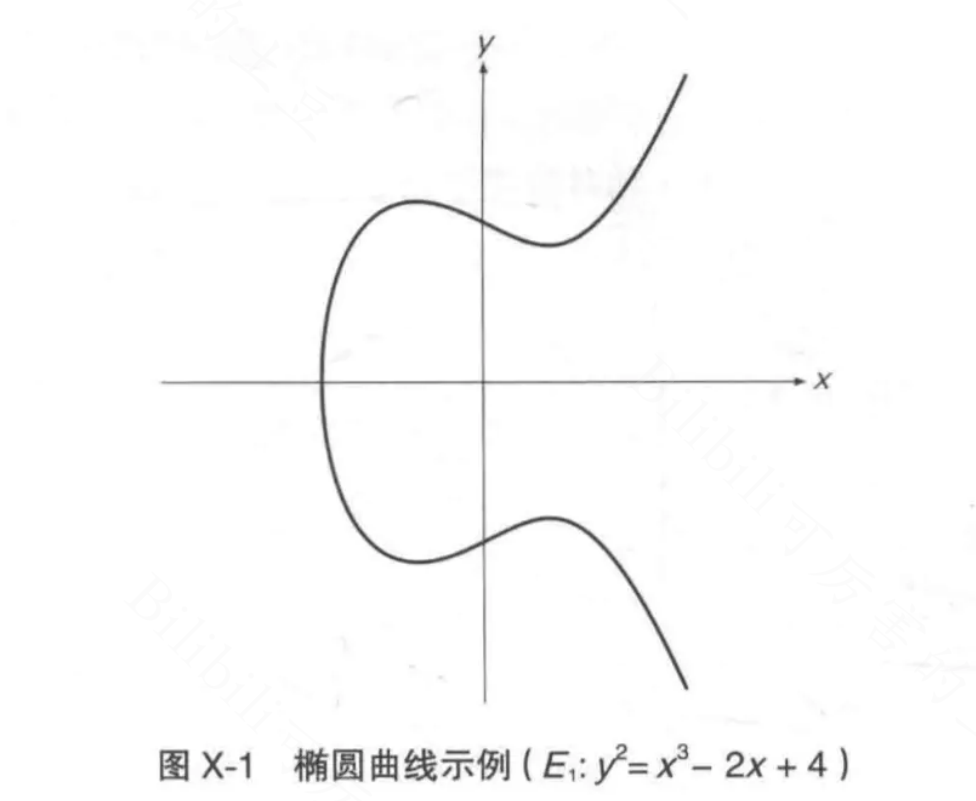
ECC-2.png

而在椭圆曲线上定义了两种运算，一种是点加，另一种是点倍。

1. 点加

点加就是两个点加的运算，但这里的加是椭圆曲线上定义的加法，并非正常使用的 1+1=2 .

举个例子，在椭圆曲线上取两个不同的点 A和B ，连接两个点并做直线交于椭圆曲线上一点，根据交点得到关于x轴对称的点，即为两个点的点加结果 A+B 。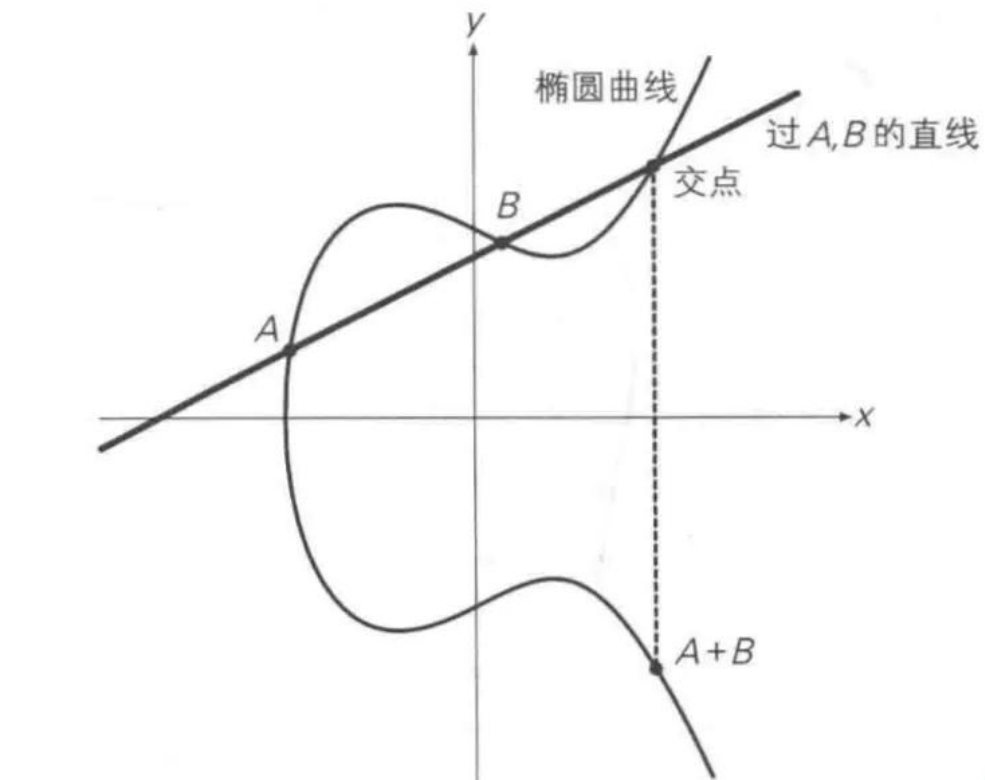
ECC-3.pngECC-4.png

2. 点倍

点倍类似于点加，选取椭圆曲线上的一个点A，作关于点的切线交椭圆曲线上的另一点，交点关于x轴堆成得到的点，即为 2A。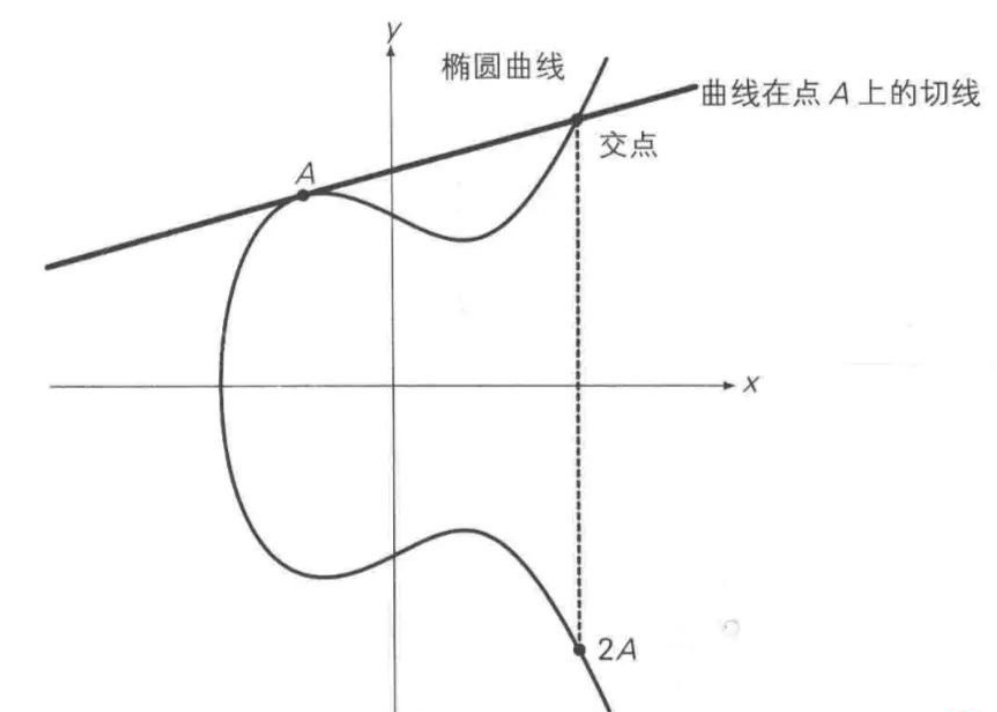
ECC-4.png

由于图象是连续的，点是无穷多个，所以需要将椭圆曲线定义在有限域上，使点的数量为有限个。

由于椭圆曲线是在有限域上，所以可以通过这条特征结合离散对数对数据进行加密。

加密

1. 定义一个椭圆曲线 Ep (a,b) 并选取一个基点 P

Ep (a,b) ，p 为有限域 mod p ，a和b为曲线中的参数a和b。

基点 P 就是点倍的首个点。

2. 选取大数 k 作为私钥并生成公钥 Q=k*P

私钥k 在现实中是很大的。

3. 选取随机数 r 并根据明文 M 生成密文 C

r 是随机数，

M 是明文，将其转为数字，一般作为 x 坐标带入到椭圆曲线 E 中求出对应的 y，然后得到 M 在椭圆曲线中的明文点 m( xM , yM )。

C 是密文，一个点对，为 ( r P , m + r Q ) ，

其中 Ep (a,b) 、P、Q 为公开的，k 为私钥保密。

解密

解密直接根据加密得到的密文进行分析，

m + r Q = m + r k P // Q = k P

r P 已知，要得到明文 M 就需要得到 m点的 x坐标，

而求 m 就需要知道 k ，

m + r k P - r P k = m // 但 k 未知

所以需要知道 k，k 求出来了，m点就好求了，m点求出来了就能得到 M ( M 为 m 的 x坐标 )。

但是由于单陷门问题求 k 很困难，所以就有了 ECC椭圆曲线加密。

附上一道例题

这是加密代码：

# 来自[HGAME_2022_week4]ECC
from Crypto.Util.number import getPrime
from libnum import s2n
from secret import flag

p = getPrime(256)
a = getPrime(256)
b = getPrime(256)
E = EllipticCurve(GF(p),[a,b])
m = E.random_point()
G = E.random_point()
k = getPrime(256)
K = k * G
r = getPrime(256)
c1 = m + r * K
c2 = r * G
cipher_left = s2n(flag[:len(flag)//2]) * m[0]
cipher_right = s2n(flag[len(flag)//2:]) * m[1]

print(f"p = {p}")
print(f"a = {a}")
print(f"b = {b}")
print(f"k = {k}")
print(f"E = {E}")
print(f"c1 = {c1}")
print(f"c2 = {c2}")
print(f"cipher_left = {cipher_left}")
print(f"cipher_right = {cipher_right}")
'''
p = 74997021559434065975272431626618720725838473091721936616560359000648651891507
a = 61739043730332859978236469007948666997510544212362386629062032094925353519657
b = 87821782818477817609882526316479721490919815013668096771992360002467657827319
k = 93653874272176107584459982058527081604083871182797816204772644509623271061231
E = Elliptic Curve defined by y^2 = x^3 + 61739043730332859978236469007948666997510544212362386629062032094925353519657*x + 12824761259043751634610094689861000765081341921946160155432001001819005935812 over Finite Field of size 74997021559434065975272431626618720725838473091721936616560359000648651891507
c1 = (14455613666211899576018835165132438102011988264607146511938249744871964946084 : 25506582570581289714612640493258299813803157561796247330693768146763035791942 : 1)
c2 = (37554871162619456709183509122673929636457622251880199235054734523782483869931 : 71392055540616736539267960989304287083629288530398474590782366384873814477806 : 1)
cipher_left = 68208062402162616009217039034331142786282678107650228761709584478779998734710
cipher_right = 27453988545002384546706933590432585006240439443312571008791835203660152890619
'''

题目是入门级的，看懂加解密过程就能解。

由于 k 已经给出来了，所以直接解密就行了。

c1 - c2 * k = m

下面是解密脚本，需要在 sage 环境下。

from sage.all import *
from Crypto.Util.number import long_to_bytes

p = 74997021559434065975272431626618720725838473091721936616560359000648651891507
a = 61739043730332859978236469007948666997510544212362386629062032094925353519657
b = 87821782818477817609882526316479721490919815013668096771992360002467657827319
k = 93653874272176107584459982058527081604083871182797816204772644509623271061231
E = EllipticCurve(GF(p),[a,b])
c1 = E([14455613666211899576018835165132438102011988264607146511938249744871964946084,25506582570581289714612640493258299813803157561796247330693768146763035791942])
c2 = E([37554871162619456709183509122673929636457622251880199235054734523782483869931,71392055540616736539267960989304287083629288530398474590782366384873814477806])
cipher_left = 68208062402162616009217039034331142786282678107650228761709584478779998734710
cipher_right = 27453988545002384546706933590432585006240439443312571008791835203660152890619

# 解密
m=c1-k*c2
cl=cipher_left//m[0]
cr=cipher_right//m[1]
cm=long_to_bytes(int(cl))+long_to_bytes(int(cr))
print(m)
print(cl)
print(cr)
print(cm)
'''
(57824879640955326550732559538097319221644125075532201058220628014917816573008 : 54475275866179647254036565579467398677511796158866832907668620448532510526757 : 1)
493033149237009446036260
127480900256551022095393917
b'hgame{Ecc$is!sO@HaRd}'
'''

最后直接解出明文

hgame{Ecc$is!sO@HaRd}

相关资料：

看的是b站博主——可厉害的土豆
个人觉得讲的还是不错的

ECC-1.png