中国剩余定理

中国剩余定理（孙子算法）

将一个数划分为两部分 —— [除数序列] [余数序列]
设：
被除数：n
除数序列： [x1, x2, x3, x4]
余数序列： [a1, a2, a3, a4]
n % x1 = a1
n % x2 = a2
n % x3 = a3
n % x4 = a4
可以通过除数和余数求出被除数 n

计算方法：

有 m = x1 x2 x3 * x4 ，exgcd( a , b ) 为 a 的逆元，
n = a1 ( m / x1 ) exgcd( m / x1 , x1 ) + a2 ( m / x2 ) exgcd( m / x2 , x2 ) + a3 ( m / x3 ) exgcd( m / x3 , x3 ) + a4 ( m / x4 ) exgcd( m / x4 , x4 ) ( mod m )

对于一般项来说，有如图所示的计算方法：

2-1

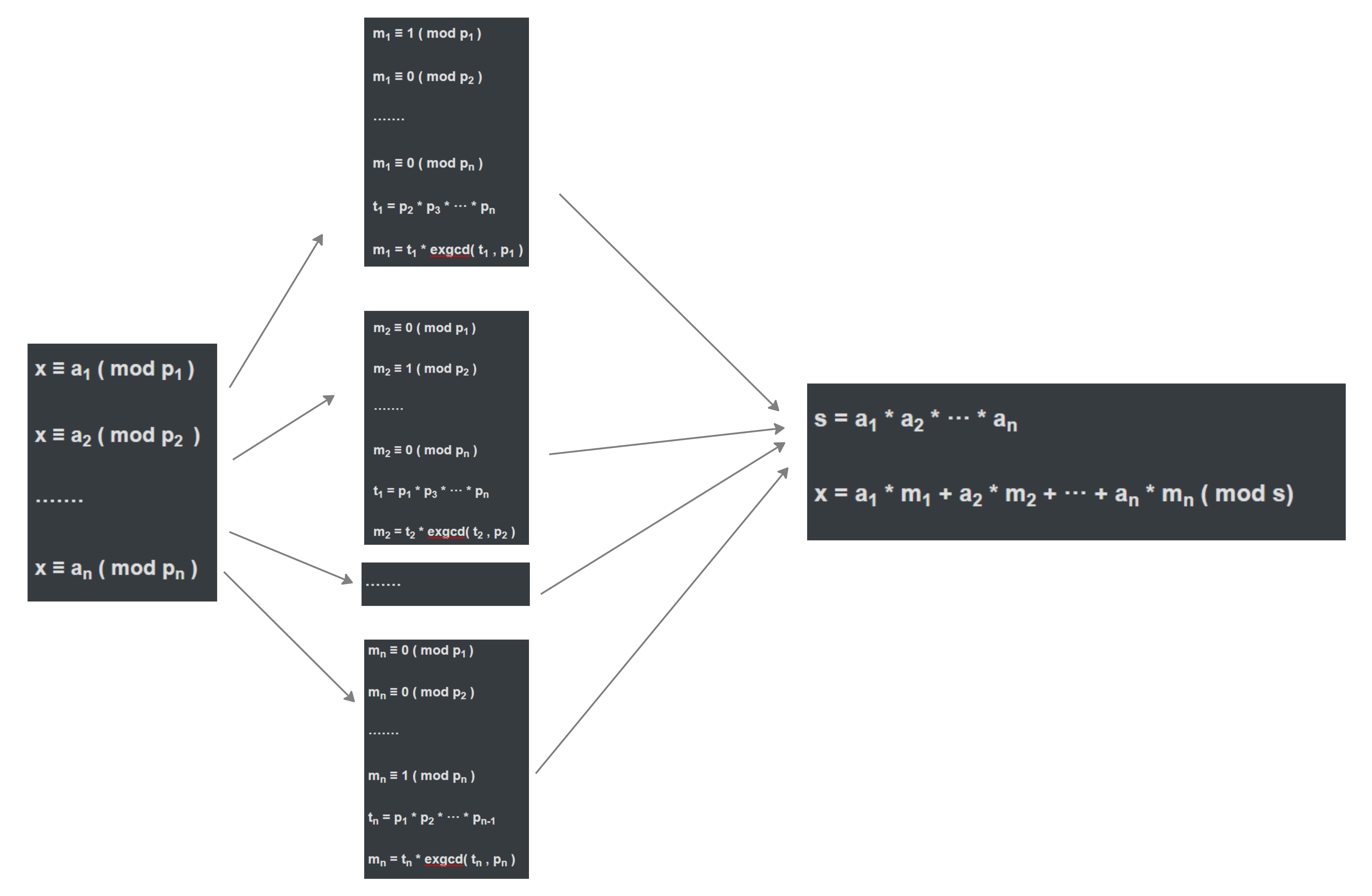
最后计算得出的值即为最小的 x ，有许多个符合上述计算的 x ，只不过这里取的是最小的一个，其余符合的数为整数倍的 s 加上最小的 x ( 即 { x | x₀ + k * s , k ∈ Z } )

例如：

已知：
k ≡ 2 ( mod 3 )
k ≡ 3 ( mod 5 )
k ≡ 2 ( mod 7 )
求出最小的 k 。
解：
通过中国剩余定理求 k
k = 2 5 7 ( -1 ) + 3 3 7 1 + 2 3 5 * 1 = -70 + 63 + 30 = 23
验算：
23 % 3 = 2
23 % 5 = 3
23 % 7 = 2
结果正确，计算正确

附上Python代码

def extend_gcd(a,b):    # 扩展欧几里得算法
    if a%b!=0:  # 如果a与b不是整除关系，则继续进行运算，否则无法得出逆元
        # 正负号处理
        sign_a, a = (-1, -a) if a < 0 else (1, a)
        sign_b, b = (-1, -b) if b < 0 else (1, b)
        # 初始化
        old_s,s=1,0
        old_t,t=0,1
        while b!=0:
            q=a//b
            old_s,s=s,old_s-s*q
            old_t,t=t,old_t-t*q
            a,b=b,a%b
        return (a,old_s*sign_a,old_t*sign_b)
    return None
def crt(a, m):        #中国剩余定理， a为余数列表，m为除数列表
    # 返回除数的乘积
    mt=1
    for i in m:
        mt*=i
    # 开始计算被除数
    s=0
    for i in range(len(a)):
        mi = mt // m[i]
        s += a[i] * mi * extend_gcd(mi,m[i])[1]
    return s%mt     # 返回被除数

中国剩余定理

附上Python代码

评论